转发:一张图弄明白:从零维到十维空间--给大神跪了 每天都是好晴天2017-07-18 13:18:32
让我们从一个点开始,和我们几何意义上的点一样,它没有大小、没有维度。它只是被想象出来的、作为标志一个位置的点。它什么也没有,空间、时间通通不存在,这就是零维度。
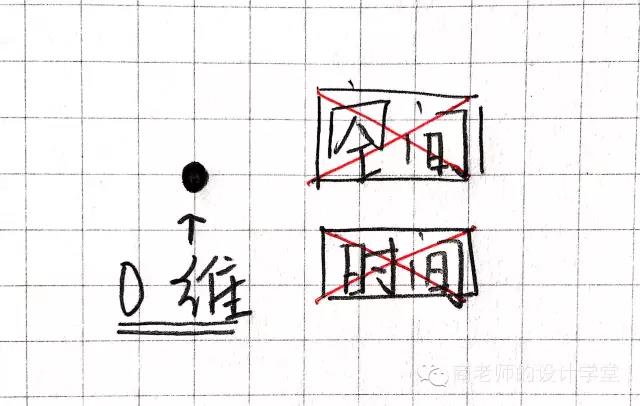
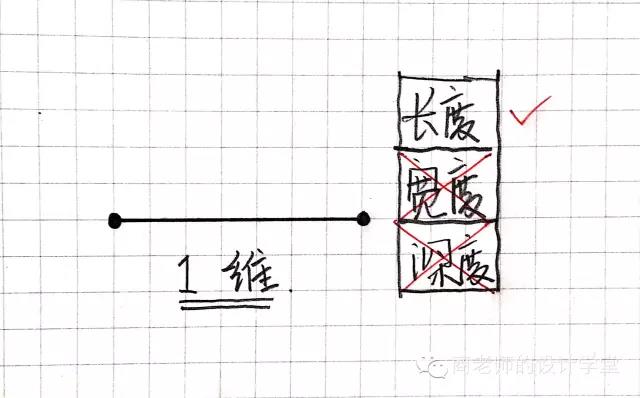
好的,理解了零维之后我们开始一维空间。已经存在了一个点,我们再画一个点。两点之间连一条线。噔噔噔!一维空间诞生了!我们创造了空间!
一维空间只有长度,没有宽度和深度。
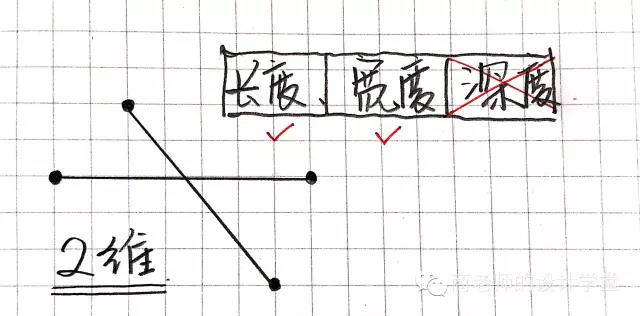
我们拥有了一条线,也就是拥有了一维空间。如何升级到二维呢?很简单,再画一条线,穿过原先的这条线,我么就有了二维空间,二维空间里的物体有宽度和长度,但是没有深度。你可以试一试,在纸上画一个长方形,长方形内部就是一个二维空间。
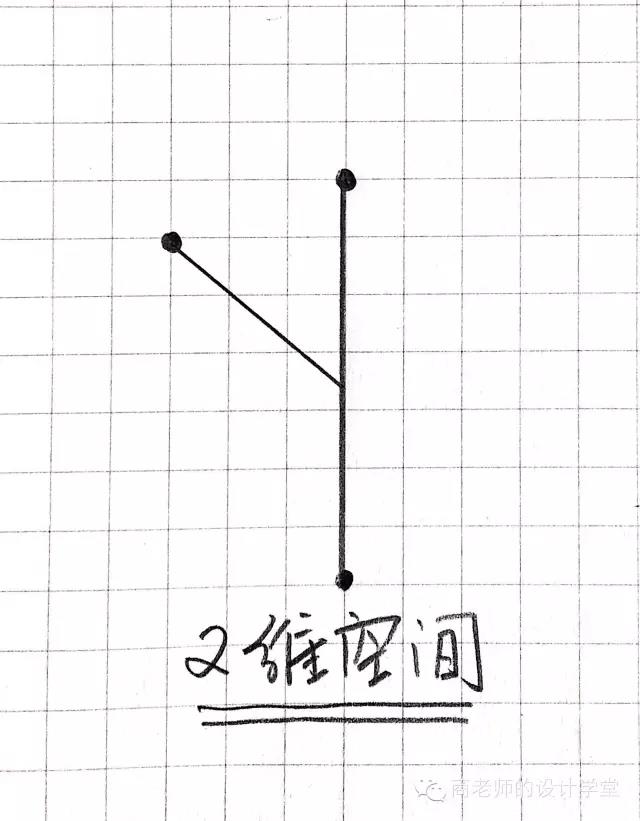
这里,为了帮助大家方便理解高维度的空间,我们用两条相交的线段来表示二维空间。
为了向更高的维度前进,现在我们现在来想象一下二维世界里的生物。因为二
维空间没有深度(也可以理解成厚度),只有长度与宽度,我们就可以将它理解成“纸片人”,或者是扑克牌K.J.A Q里的画像。因为维度的局限,这个可怜的二维生物也只能看到二维的形状。如果让它去看一个三维的球体,那么他只能看到的是这个球体的截面,也就是一个圆。
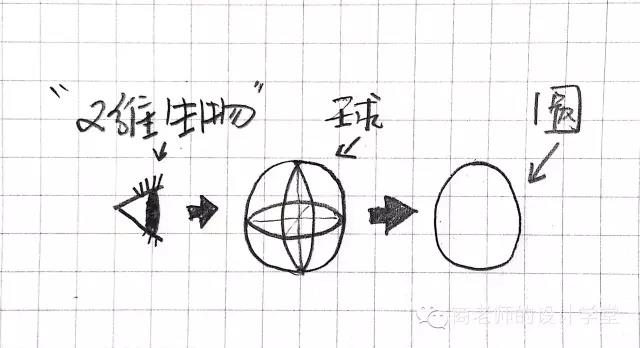
三维空间大家肯定熟悉,我们无时无刻都生活在三维空间中。三维空间有长度、宽度与高度。
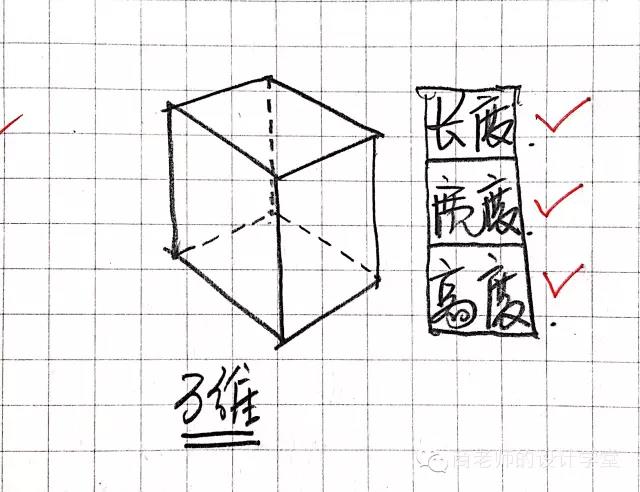
但是,我要用另一种思维来表达三维空间,只有这样,才可以向更高维度推进。
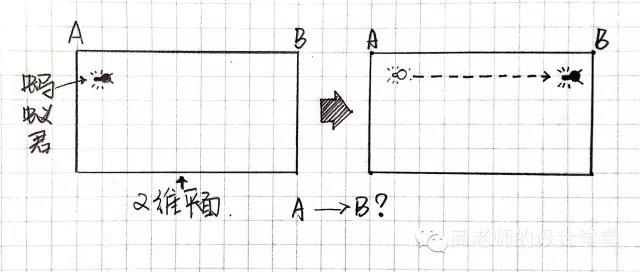
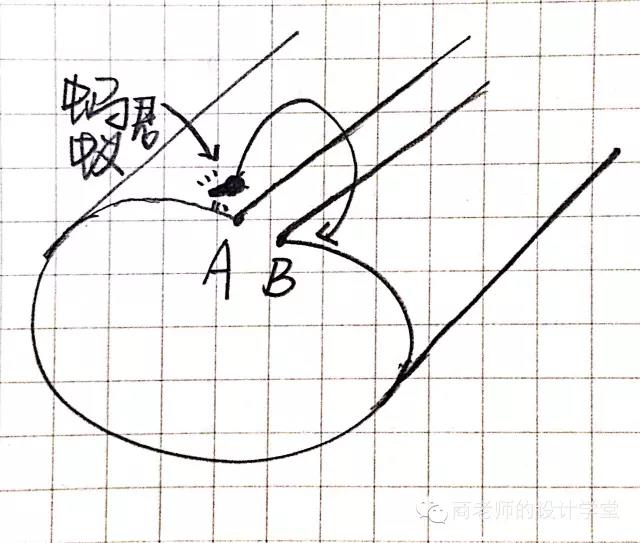
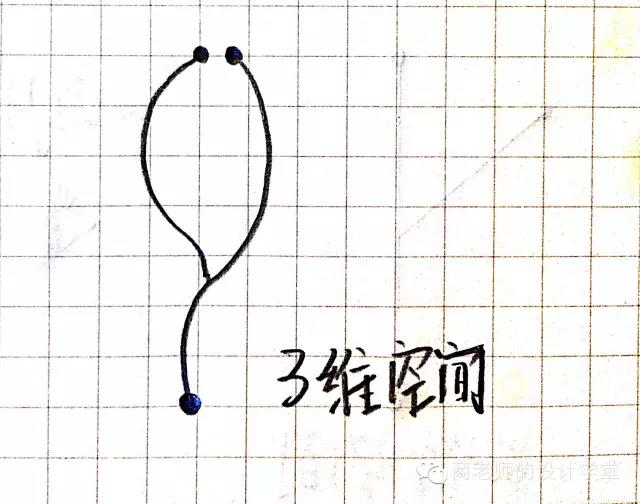
好,现在我们有一张报纸,上面有一只蚂蚁。我们就姑且把蚂蚁君看作是“二维生物”,我在二维的纸面上移动。如果要让他从纸的一边爬到另一边,则蚂蚁君需要走过整个纸张。但是我们把这张纸卷起来呢?成为一个圆柱,一个三维空间里的物体;这时蚂蚁君只需要走过接缝的位置,就到达了目的地。(对了!就是传说中的虫洞)换句话说,把二维空间弯曲,就得到了三维空间,我们就可以这样来表达。
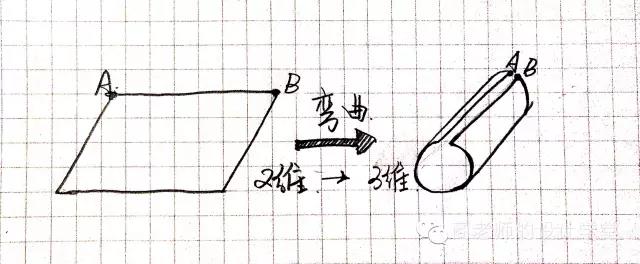
再解释一遍,在这个图示上,蚂蚁从A点消失,B点出现,你们想想,就是这意思,卷曲产生新的维度!

好了,
开始进入烧脑阶段!
前三个维度我们可以简单理解成长、宽、高。那么我们怎么理解四维空间?
四维比三维多一维,它是什么?是时间!
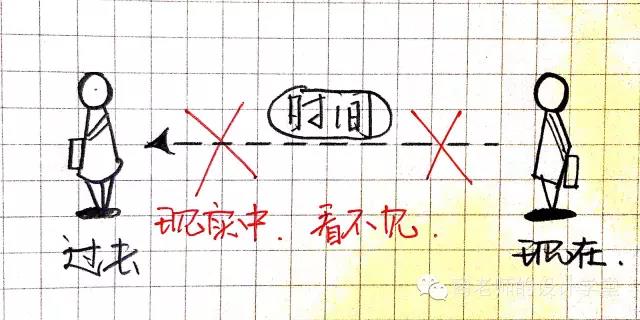
想象一下,左边有一个1分钟之前的我,右边则是现在我,将这“两个我”看成两个点 ,穿过他们连线,它就是四维空间里的线。太棒了,四维空间出现了!

那么在现实当中我们可以看到过去和未来的我么?不能!因为我们是三维生物,活在三维空间中。 就像上文提到的,那位二维生物只能看到三维物体的截面一样,我们作为三维生物,只能看到四维空间的截面,也就是现在的你、我、他;换句话说就是此时此刻的世界 。
你们还可以么?
我要开始讲五维空间了哦
首先我们要明确一点,低维度生物不能意识到高维度空间发生的事情。我们从出生到现在,都感觉自己在同一个空间里。我们常说“随着时间的推移”,其实就是沿着时间线向前,这条时间线就是四维空间里的那条线,换句话说,三维的我们沿着四维空间里的时间线向前走。
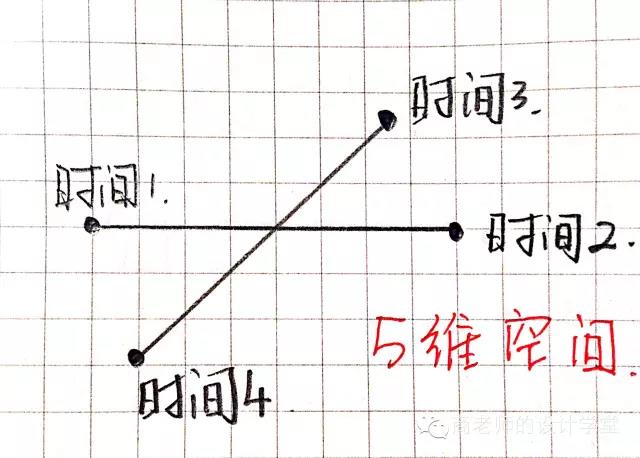
假如我们是四维空间生物,我们就可以看到过去、现在、将来各个时段的我们自己。但是,时间线只有一条,还记得前文中两条线交叉,将一维升级为二维么?那么现在,在四维这条时间线的基础上,我再加一条时间线和这条时间线交叉,五维空间就出现了!
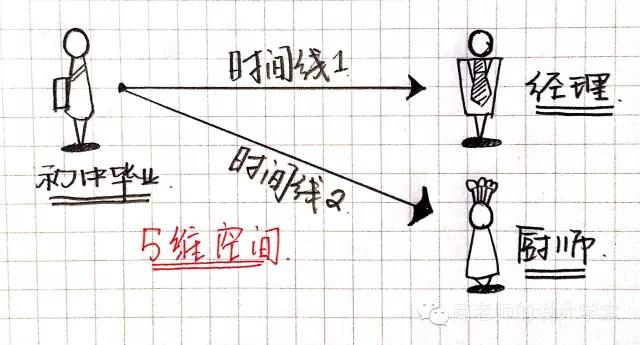
不懂?没关系!例子举起来!比如说,你大学毕业参加工作,工作了5年,现在是一名经理,那么四维空间里你只能看到大学毕业的你以及成为白领的这条时间线上的你。 如果当初你初中毕业就去学烹饪,现在是一名厨师。那么这就是另一条时间线上的你。
在五维空间中,你可以看到成为经理的你,也可以看到成为厨师的你。总结的说,五维空间,你可以看到你未来的不同分支。
六维空间
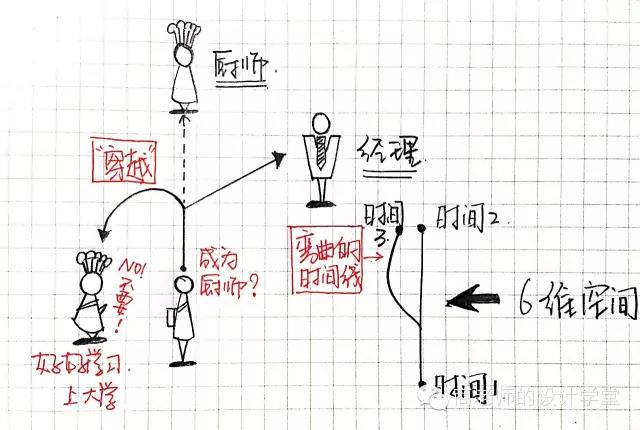
OK 我开始解释六维空间。现在的你如果想拜访一下过去的你,怎么办?我们可以将四维空间中任意一条时间线弯曲,这样你就可以跳回以前,去见以前的你。换句话说,五维空间中,你可以“穿越”回到一条时间线上的过去。
还是拿“经理的你”和“厨师的你”举例子,厨师的你感觉日子很艰辛,每天油烟呛人,你想成为经理,安安静静在办公室里坐着。怎么办?五维空间中,你可以穿越到你初中毕业的时候,告诉以前的你,一定要继续读书,上高中,考大学,做白领。不过这很费力,而且风险很大,初中毕业的你需要作出不同的选择,每一种选择都会产生一个新的时间线,一个不同版本的未来。
你们还记得二维空间中蚂蚁君和报纸么?弯曲一个空间产生一个新的维度。对了!我们直接把五维空间弯曲,产生六维空间。这样,你就可以穿越到“经理的你”这条时间线,看一看另一个版本的你。
如果你能看到这里,恭喜你,你的脑洞已经很大了。
好,我们继续,七维空间走起来。还是那个例子,前面提到两个时间线:经理与厨师。初中毕业的你,不可能只有这两种选择,而是近乎无限。怎么解释,你的每一个决定都在塑造出一个特有的你。你可以成为任何一种你。概括地说,初中毕业的你是一个起点,所有的时间线。都从这个点向外辐射,数量是无穷大,那么最后,七维空间里的一个点,里面包含着“初中毕业的你”开始的无限种可能。
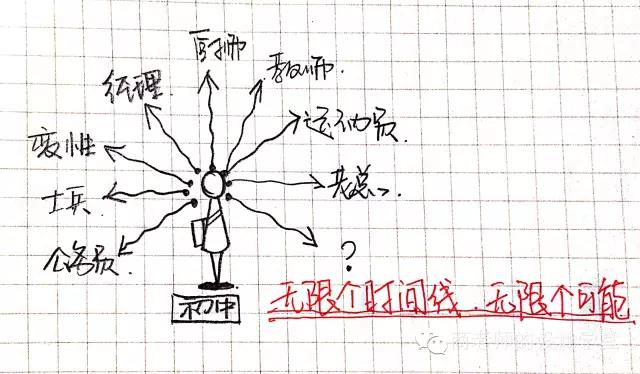

那么怎么画出七维空间里的一条线?我们需要另一个点,但是这个点已经包含了无限,如何再去找另外一个点?那就是另一种开端。
没关系,我们举例子,你会懂得。前文中我们提到由“初中毕业的你”为开端而产生的七维无限点;如果你小学毕业的时候就作出不同的选择呢?每一个选择又会塑造一个不同的你;那么以“小学毕业的你”为开端,就会产生另一个包含着无限时间线的点。将这两点连成一条线,就是七维空间的线。
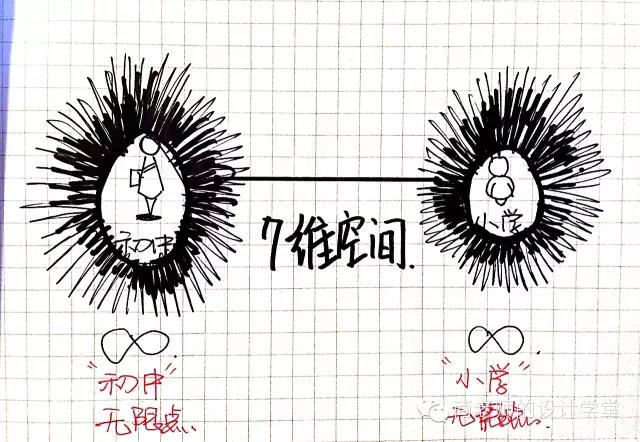
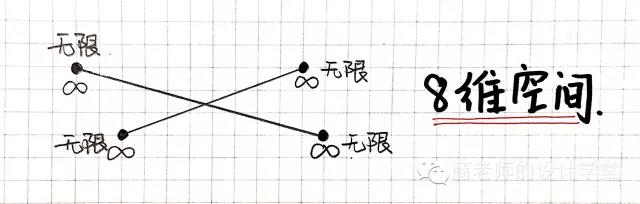
还记得文章开始时提到的一维的线么?我们把另外一条线穿过它,就变成了二维空间。同样的道理,我们来给七维空间升级。例子呢,还是那个“你”。我们又找到了两个点,一个是由“大学毕业的你”为开端产生的七维无限点,另一个是由“50岁的你”为开端产生的无限点。将这两点连线,与上文中那条连接“初中毕业的你”无限点“小学毕业的你”无限点的这条线相交。我们就得到了八维空间!
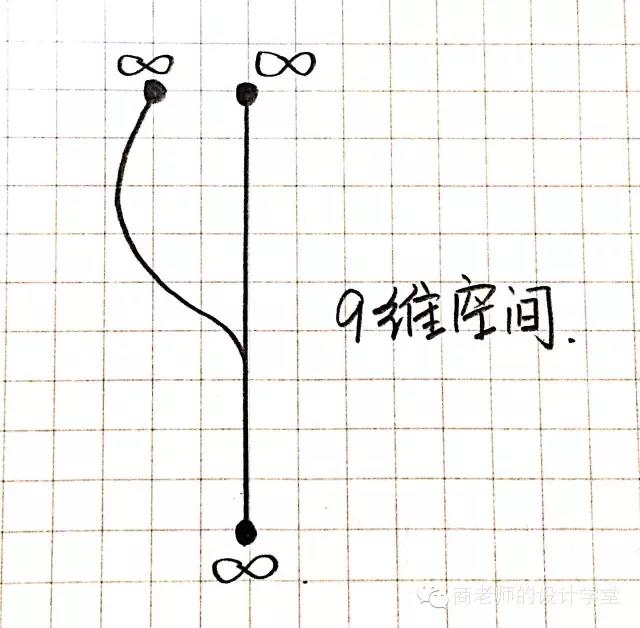
好了,讲到这里,你其实可以想象出九维空间是什么样了。我们把八维空间理解成那张报纸,平平的。这时蚂蚁君又出现了,不过它已经进化成八维空间生物了,给它一样的任务,要他横跨整个报纸去目的地,怎么办?将报纸再一次卷起来,虫洞又出现了。蚂蚁君顺利穿过虫洞出现在目的地。也就是说,将八维空间继续卷曲,我们就得到了九维空间!
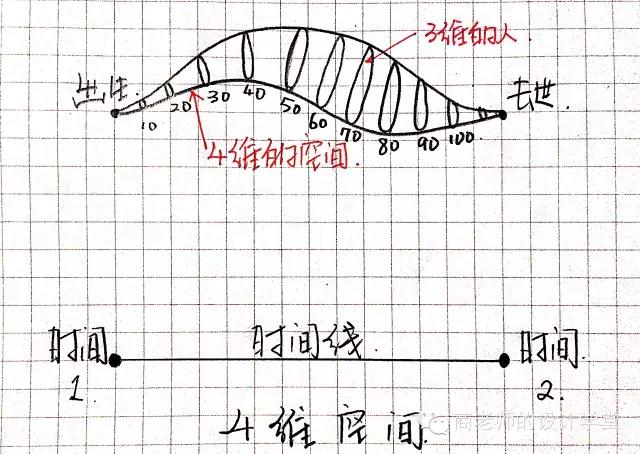
这里我来总结一下,回顾上文,从零维到四维,我们经历了点、线、面、体这个升级流程。然后四维空间又可以看做一点,充满着三维空间中所有可能性的连线,这个连线就是时间。
从四维到八维,我们又经历了点、线、面、体的升级流程。八维的点,充满着七维空间中所有可能性的连线。
八维空间继续升级。还是那个“你”,以八维空间的点为起始,我们必须想出所有的可能,每一种可能都与八维的这个点相连,最后,我们得到十维空间里的一个点,充满着九维空间中所有可能性的连线。
还能再升级么?不能了,在十维空间中,我们找不到任何一个空间可以在划出一个点,因为,十维空间就是一个点!
它包含着所有的宇宙、所有的可能性、所有的时间线、所有的所有...........

从零位到十维,我们经历了这么多,
最后,它还是一个点
......
有趣吗?
虚无回归到无穷可能,无所不包